Na Slovensku, ale aj zahraničí sa pomerne často používajú metódy nepriamo stanovenia maximálnych prietokov, pretože na mnohých menších povodiach neexistujú pravidelné merania ich história. Ich výhoda spočíva najmä v absencii náročných a časovo dlhších terénnych meraní na tokoch a v povodiach. Takto získané údaje samozrejme obsahujú istú mieru nepresnosti, ktorá však môže byť korigovaná expertným odhadom odborníka a tým sa modelovaný výsledok stanovený empirickým vzorcom čo najviac približuje k výsledkom z modelovania prostredníctvom presných údajov z terénu. Tiež treba konštatovať, že pre spoľahlivý odhad 100 ročného maximálneho prietoku je potrebný pozorovací rad dlhý aspoň 500 rokov.
Empirické vzorce sa najčastejšie kategorizujú do troch tried: regionálne, objemové a intenzívne. V podmienkach Slovenska a Česka sú najčastejšie používané regionálne vzorce. Vychádzajú z empirických skúseností, že špecifický odtok Qmax klesá s rastom plochy povodia, pričom nejde o lineárny vzťah. Špecifický odtok je objem odtoku vody z jednotky plochy za jednotku času. Medzi známe vzorce a postupy pri stanovení Qmax patria regionálne vzorce (Dub, 1957; Hlubocký, 1977; Čermák, 1956; Čermák, 1962; Makeľ a kol., 2003). Aj napriek ich staršiemu datovaniu sú stále často používané a len niekoľko prác sa ich pokúšalo spresniť, či modifikovať (Kohnová & Szolgay, 1995; Makeľ a kol., 2003). Oblastné empirické vzorce nie celkom dobre vyhovujú určeniu Q100 na úplne malých povodiach a výrazne nadhodnocujú hodnoty storočného maximálneho špecifického odtoku (Solín, 2005).
V našich podmienkach sú stále často aplikované regionálne vzorce (Pekárová a kol., 2011; Jakubis, 2015; Čunderlík, 1997). Pri rozbore vzniku maximálneho prietoku a účasti hlavných činiteľov na ňom sa ukázalo, že za predpokladu rovnakých podmienok výskytu intenzívnych dažďov a rovnakých odtokových podmienok zostane rozhodujúcim činiteľom plocha povodia (Dub, 1957). Maximálny špecifických odtok klesá so zväčšujúcou sa plochou povodia.
Celý text článku je momentálne uzamknutý. Pre jeho odomknutie a pokračovanie ma môžete kontaktovať.
Ukážka spracovania pre modelové územie povodia Halča
Ukážka spracovania záujmového územia v HEC-RAS – geometria tokov povodia
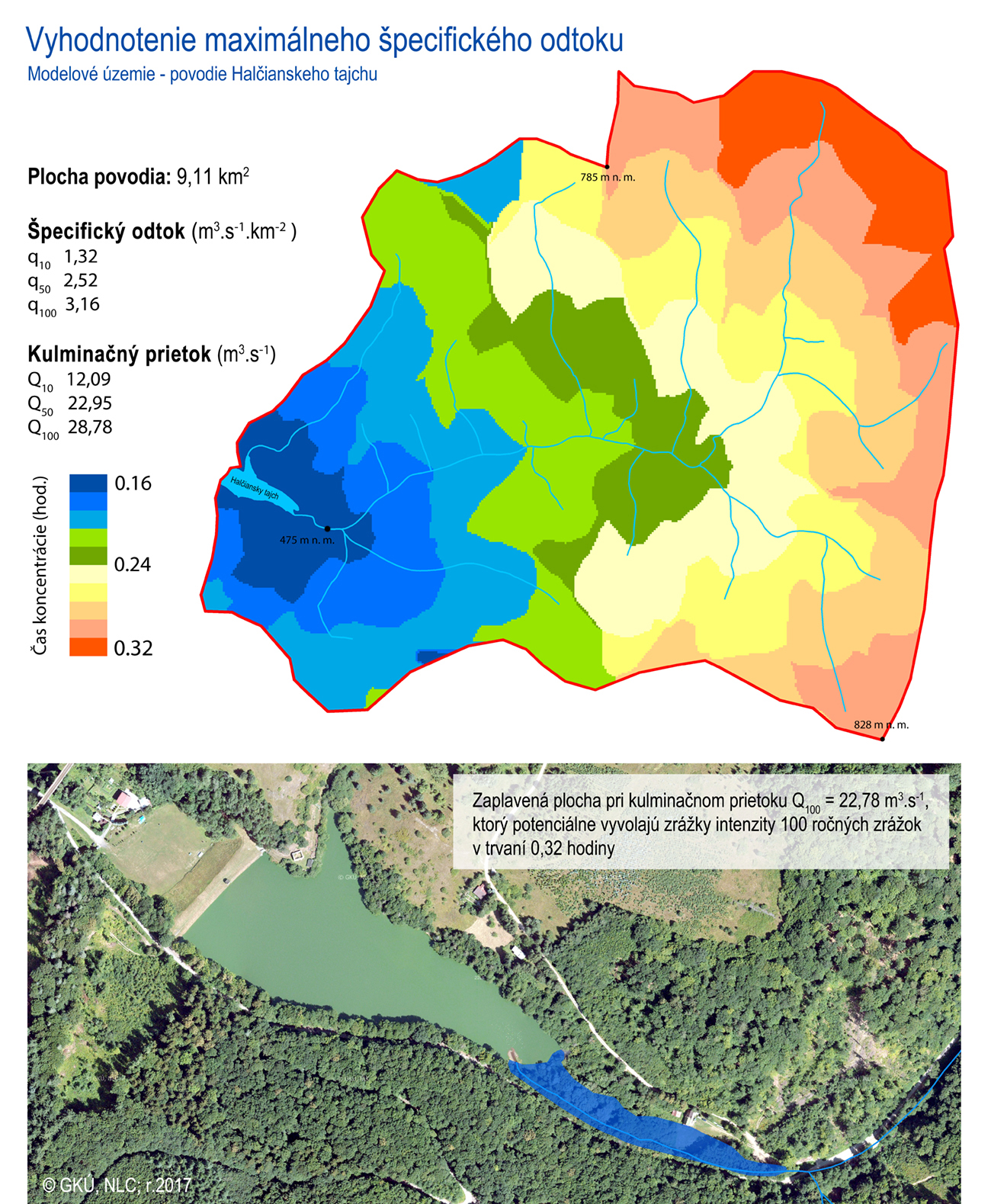
Nasledovná príloha tvorí ukážku spracovania výpočtov maximálneho špecifického odtoku a kulminačného prietoku Q10, Q50 a Q100 v povodí Halčianskeho tajchu pri Banskej Štiavnici, vrátane vizualizácie potenciálneho zaplavenia územia v spodnej časti povodia pri kulminačnom prietoku Q100, ktorá bola spracovaná v softvérovom prostredí HEC-RAS. V tomto ukážkovom modelovaní platí:
1) doba trvania zrážok je rovnako dlhá ako doba koncentrácie
2) intenzita zrážok je rovnaká v celom povodí
3) potenciálna povodňová vlna je spôsobená zrážkami s danou významnosťou (N-ročnosťou) 100
Obrázok 8: Ukážka spracovania pre modelové územie povodia Halča
V prípade, že sa zaoberáte vo svojej práci GIS modelovaním a hľadáte spracovateľa aj takýchto modelov, kontaktujte ma.
Pridať komentár k článku